1. \(\frac{3}{2}nBA\omega\)
2. \(3nBA\omega\)
3. \(nBA\omega\)
4. \(\frac{1}{2}nBA\omega\)
A very long solenoid of radius \(R\) is carrying current \(I(t)=k t e^{-\alpha t}(k>0),\) as a function of time \((t\geq0).\) Counter clockwise current is taken to be positive. A circular conducting coil of radius \(2R\) is placed in the equatorial plane of the solenoid and concentric with the solenoid. The current induced in the outer coil is correctly depicted, as a function of time, by:
| 1. | 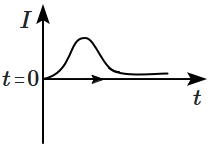 |
2. |  |
| 3. |  |
4. |  |
1. \(0.14~\text{mC}\)
2. \(0.7~\text{mC}\)
3. \(0.21~\text{mC}\)
4. \(0.6~\text{mC}\)
A uniform magnetic field \(B\) exists in a direction perpendicular to the plane of a square loop made of a metal wire. The wire has a diameter of \(4~\text{mm}\) and a total length of \(30~\text{cm}\). The magnetic field changes with time at a steady rate \(\frac{dB}{dt}=0.032~ \text{Ts}^{-1}\). The induced current in the loop is close to:(the resistivity of the metal wire is \(1.23\times 10^{-8}~\Omega\text{m}\))
1. \(0.34 ~\text{A}\)
2. \(0.53 ~\text{A}\)
3. \(0.61~\text{A}\)
4. \(0.43~\text{A}\)
A small bar magnet is moved through a coil at constant speed from one end to the other. Which of the following series of observations will be seen on the galvanometer \(G\) attached across the coil ?
Three positions shown describe : (a) the magnet's entry (b) magnet is completely inside and (c) magnet's exit.
| 1. | 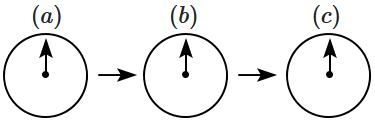 |
| 2. | 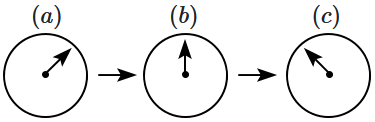 |
| 3. | 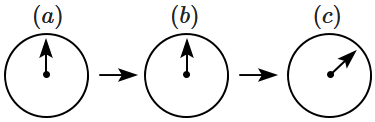 |
| 4. | 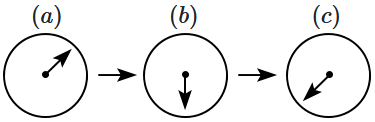 |
Two concentric circular coils, \(C_1\) and \(C_2\), are placed in the \(XY\) plane. \(C_1\) has \(500\) turns, and a radius of \(1\) cm. \(C_2\) has \(200\) turns and radius of \(20\) cm. \(C_2\) carries a time dependent current \(I(t)=\left(5 t^2-2 t+3\right) \text{A}\) where \(t\) is in \(s\). The emf induced in \(C_1\) (in mV), at the instant \(t=1~\mathrm{s}\) is \(\frac{4}{x}\). The value of \(x\) is:
1. \(3\)
2. \(5\)
3. \(7\)
4. \(9\)
1. \(15.6~\text A\)
2. \(16.6~\text A\)
3. \(17.6~\text A\)
4. \(18.6~\text A\)
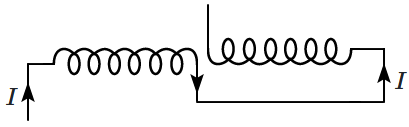
1. \(\frac{1}{L_1}+\frac{1}{L_2}+\frac{1}{M}\)
2. \(L_1+L_2+M\)
3. \(L_1+L_2+2 M\)
4. \(L_1+L_2-2M\)
1. Halved
2. Quadrupled
3. The same
4. Doubled
1. \(150\) mA
2. \(300\) mA
3. \(250\) mA
4. \(100\) mA